ndian mathematics emerged in the Indian subcontinent[1] from 1200 BC[2] until the end of the 18th century. In the classical period of Indian mathematics (400 AD to 1200 AD), important contributions were made by scholars like Aryabhata, Brahmagupta, and Bhaskara II. Although the decimal number system first appeared in Egypt, the modern numeration system in use today[3] was first recorded in Indian mathematics.[4] Indian mathematicians made early contributions to the study of the concept of zero as a number,[5] the law of signs for multiplication and division in arithmetic,[6] and the Hindu-Arabic numeral system.[7] In addition, trigonometry[8] was further advanced in India, and, in particular, the modern definitions of sine and cosine were developed there.[9] These mathematical concepts were transmitted to the Middle East, China, and Europe[10] and led to further developments that now form the foundations of many areas of mathematics.
Ancient and medieval Indian mathematical works, all composed in Sanskrit, usually consisted of a section of sutras in which a set of rules or problems were stated with great economy in verse in order to aid memorization by a student. This was followed by a second section consisting of a prose commentary (sometimes multiple commentaries by different scholars) that explained the problem in more detail and provided justification for the solution. In the prose section, the form (and therefore its memorization) was not considered so important as the ideas involved.[1][11] All mathematical works were orally transmitted until approximately 500 BCE; thereafter, they were transmitted both orally and in manuscript form. The oldest extant mathematical document produced on the Indian subcontinent is the birch bark Bakhshali Manuscript, discovered in 1881 in the village of Bakhshali, near Peshawar (modern day Pakistan) and is likely from the 7th century CE.[12][13]
A later landmark in Indian mathematics was the development of the series expansions for trigonometric functions (sine, cosine, and arc tangent) by mathematicians of the Kerala school in the 15th century CE. Their remarkable work, completed two centuries before the invention of calculus in Europe, provided what is now considered the first example of a power series (apart from geometric series).[14]However, they did not formulate a systematic theory of differentiation and integration, nor is there any direct evidence of their results being transmitted outside Kerala.[15][16][17][18]
Prehistory[edit]
Excavations at Harappa, Mohenjo-daro and other sites of the Indus Valley Civilization have uncovered evidence of the use of "practical mathematics". The people of the IVC manufactured bricks whose dimensions were in the proportion 4:2:1, considered favourable for the stability of a brick structure. They used a standardized system of weights based on the ratios: 1/20, 1/10, 1/5, 1/2, 1, 2, 5, 10, 20, 50, 100, 200, and 500, with the unit weight equaling approximately 28 grams (and approximately equal to the English ounce or Greek uncia). They mass-produced weights in regular geometrical shapes, which included hexahedra, barrels, cones, and cylinders, thereby demonstrating knowledge of basic geometry.[19]
The inhabitants of Indus civilisation also tried to standardise measurement of length to a high degree of accuracy. They designed a ruler—the Mohenjo-daro ruler—whose unit of length (approximately 1.32 inches or 3.4 centimetres) was divided into ten equal parts. Bricks manufactured in ancient Mohenjo-daro often had dimensions that were integral multiples of this unit of length.[20][21]
Samhitas and Brahmanas[edit]
The religious texts of the Vedic Period provide evidence for the use of large numbers. By the time of the Yajurvedasaṃhitā- (1200–900 BCE), numbers as high as 1012 were being included in the texts.[2] For example, the mantra (sacrificial formula) at the end of theannahoma ("food-oblation rite") performed during the aśvamedha, and uttered just before-, during-, and just after sunrise, invokes powers of ten from a hundred to a trillion:[2]
"Hail to śata ("hundred," 102), hail to sahasra ("thousand," 103), hail to ayuta ("ten thousand," 104), hail to niyuta ("hundred thousand," 105), hail to prayuta ("million," 106), hail to arbuda ("ten million," 107), hail to nyarbuda ("hundred million," 108), hail tosamudra ("billion," 109, literally "ocean"), hail to madhya ("ten billion," 1010, literally "middle"), hail to anta ("hundred billion,"1011,lit., "end"), hail to parārdha ("one trillion," 1012 lit., "beyond parts"), hail to the dawn (us'as), hail to the twilight (vyuṣṭi), hail to the one which is going to rise (udeṣyat), hail to the one which is rising (udyat), hail to the one which has just risen (udita), hail tosvarga (the heaven), hail to martya (the world), hail to all."[2]
The Satapatha Brahmana (ca. 7th century BCE) contains rules for ritual geometric constructions that are similar to the Sulba Sutras.[22]
Vedic period[edit|edit source]
Samhitas and Brahmanas[edit]
The religious texts of the Vedic Period provide evidence for the use of large numbers. By the time of the Yajurvedasaṃhitā- (1200–900 BCE), numbers as high as 1012 were being included in the texts.[2] For example, the mantra (sacrificial formula) at the end of theannahoma ("food-oblation rite") performed during the aśvamedha, and uttered just before-, during-, and just after sunrise, invokes powers of ten from a hundred to a trillion:[2]
"Hail to śata ("hundred," 102), hail to sahasra ("thousand," 103), hail to ayuta ("ten thousand," 104), hail to niyuta ("hundred thousand," 105), hail to prayuta ("million," 106), hail to arbuda ("ten million," 107), hail to nyarbuda ("hundred million," 108), hail tosamudra ("billion," 109, literally "ocean"), hail to madhya ("ten billion," 1010, literally "middle"), hail to anta ("hundred billion,"1011,lit., "end"), hail to parārdha ("one trillion," 1012 lit., "beyond parts"), hail to the dawn (us'as), hail to the twilight (vyuṣṭi), hail to the one which is going to rise (udeṣyat), hail to the one which is rising (udyat), hail to the one which has just risen (udita), hail tosvarga (the heaven), hail to martya (the world), hail to all."[2]
The Satapatha Brahmana (ca. 7th century BCE) contains rules for ritual geometric constructions that are similar to the Sulba Sutras.[22]
Śulba Sūtras[edit]
Main article: Śulba Sūtras
The Śulba Sūtras (literally, "Aphorisms of the Chords" in Vedic Sanskrit) (c. 700–400 BCE) list rules for the construction of sacrificial fire altars.[23] Most mathematical problems considered in the Śulba Sūtras spring from "a single theological requirement,"[24] that of constructing fire altars which have different shapes but occupy the same area. The altars were required to be constructed of five layers of burnt brick, with the further condition that each layer consist of 200 bricks and that no two adjacent layers have congruent arrangements of bricks.[24]
According to (Hayashi 2005, p. 363), the Śulba Sūtras contain "the earliest extant verbal expression of the Pythagorean Theorem in the world, although it had already been known to the Old Babylonians."
The diagonal rope (akṣṇayā-rajju) of an oblong (rectangle) produces both which the flank (pārśvamāni) and the horizontal (tiryaṇmānī) <ropes> produce separately."[25]
Since the statement is a sūtra, it is necessarily compressed and what the ropes produce is not elaborated on, but the context clearly implies the square areas constructed on their lengths, and would have been explained so by the teacher to the student.[25]
They contain lists of Pythagorean triples,[26] which are particular cases of Diophantine equations.[27] They also contain statements (that with hindsight we know to be approximate) about squaring the circle and "circling the square."[28]
Baudhayana (c. 8th century BCE) composed the Baudhayana Sulba Sutra, the best-known Sulba Sutra, which contains examples of simple Pythagorean triples, such as: (3, 4, 5),(5, 12, 13), (8, 15, 17), (7, 24, 25), and (12, 35, 37),[29] as well as a statement of the Pythagorean theorem for the sides of a square: "The rope which is stretched across the diagonal of a square produces an area double the size of the original square."[29] It also contains the general statement of the Pythagorean theorem (for the sides of a rectangle): "The rope stretched along the length of the diagonal of a rectangle makes an area which the vertical and horizontal sides make together."[29] Baudhayana gives a formula for thesquare root of two,[30]
The formula is accurate up to five decimal places, the true value being 1.41421356...[31] This formula is similar in structure to the formula found on a Mesopotamian tablet[32] from the Old Babylonian period (1900–1600 BCE):[30]
which expresses √2 in the sexagesimal system, and which is also accurate up to 5 decimal places (after rounding).
According to mathematician S. G. Dani, the Babylonian cuneiform tablet Plimpton 322 written ca. 1850 BCE[33] "contains fifteen Pythagorean triples with quite large entries, including (13500, 12709, 18541) which is a primitive triple,[34] indicating, in particular, that there was sophisticated understanding on the topic" in Mesopotamia in 1850 BCE. "Since these tablets predate the Sulbasutras period by several centuries, taking into account the contextual appearance of some of the triples, it is reasonable to expect that similar understanding would have been there in India."[35] Dani goes on to say:
"As the main objective of the Sulvasutras was to describe the constructions of altars and the geometric principles involved in them, the subject of Pythagorean triples, even if it had been well understood may still not have featured in the Sulvasutras. The occurrence of the triples in the Sulvasutras is comparable to mathematics that one may encounter in an introductory book on architecture or another similar applied area, and would not correspond directly to the overall knowledge on the topic at that time. Since, unfortunately, no other contemporaneous sources have been found it may never be possible to settle this issue satisfactorily."[35]
In all, three Sulba Sutras were composed. The remaining two, the Manava Sulba Sutra composed by Manava (fl. 750–650 BC) and the Apastamba Sulba Sutra, composed byApastamba (c. 600 BC), contained results similar to the Baudhayana Sulba Sutra.
- Vyakarana
An important landmark of the Vedic period was the work of Sanskrit grammarian, Pāṇini (c. 520–460 BCE). His grammar includes early use of Boolean logic, of the null operator, and of context free grammars, and includes a precursor of the Backus–Naur form (used in the description programming languages).
Pingala[edit]
Among the scholars of the post-Vedic period who contributed to mathematics, the most notable is Pingala (piṅgalá) (fl. 300–200 BCE), a musical theorist who authored theChhandas Shastra (chandaḥ-śāstra, also Chhandas Sutra chhandaḥ-sūtra), a Sanskrit treatise on prosody. There is evidence that in his work on the enumeration of syllabic combinations, Pingala stumbled upon both the Pascal triangle and Binomial coefficients, although he did not have knowledge of the Binomial theorem itself.[36][37] Pingala's work also contains the basic ideas of Fibonacci numbers (called maatraameru). Although the Chandah sutra hasn't survived in its entirety, a 10th-century commentary on it by Halāyudha has. Halāyudha, who refers to the Pascal triangle as Meru-prastāra (literally "the staircase to Mount Meru"), has this to say:
"Draw a square. Beginning at half the square, draw two other similar squares below it; below these two, three other squares, and so on. The marking should be started by putting 1 in the first square. Put 1 in each of the two squares of the second line. In the third line put 1 in the two squares at the ends and, in the middle square, the sum of the digits in the two squares lying above it. In the fourth line put 1 in the two squares at the ends. In the middle ones put the sum of the digits in the two squares above each. Proceed in this way. Of these lines, the second gives the combinations with one syllable, the third the combinations with two syllables, ..."[36]
The text also indicates that Pingala was aware of the combinatorial identity:[37]
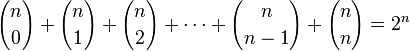
- Katyayana
Katyayana (c. 3rd century BCE) is notable for being the last of the Vedic mathematicians. He wrote the Katyayana Sulba Sutra, which presented much geometry, including the general Pythagorean theorem and a computation of the square root of 2 correct to five decimal places.
Jain Mathematics (400 BCE – 200 CE)[edit]
Although Jainism as a religion and philosophy predates its most famous exponent, Mahavira (6th century BCE), who was a contemporary of Gautama Buddha, most Jaina texts on mathematical topics were composed after the 6th century BCE. Jaina mathematicians are important historically as crucial links between the mathematics of the Vedic period and that of the "Classical period."
A significant historical contribution of Jaina mathematicians lay in their freeing Indian mathematics from its religious and ritualistic constraints. In particular, their fascination with the enumeration of very large numbers and infinities, led them to classify numbers into three classes: enumerable, innumerable and infinite. Not content with a simple notion of infinity, they went on to define five different types of infinity: the infinite in one direction, the infinite in two directions, the infinite in area, the infinite everywhere, and the infinite perpetually. In addition, Jaina mathematicians devised notations for simple powers (and exponents) of numbers like squares and cubes, which enabled them to define simple algebraic equations(beejganita samikaran). Jaina mathematicians were apparently also the first to use the word shunya (literally void in Sanskrit) to refer to zero. More than a millennium later, their appellation became the English word "zero" after a tortuous journey of translations and transliterations from India to Europe . (See Zero: Etymology.)
In addition to Surya Prajnapti, important Jaina works on mathematics included the Vaishali Ganit (c. 3rd century BCE); the Sthananga Sutra (fl. 300 BCE – 200 CE); theAnoyogdwar Sutra (fl. 200 BCE – 100 CE); and the Satkhandagama (c. 2nd century CE). Important Jaina mathematicians included Bhadrabahu (d. 298 BCE), the author of two astronomical works, the Bhadrabahavi-Samhita and a commentary on the Surya Prajinapti; Yativrisham Acharya (c. 176 BCE), who authored a mathematical text calledTiloyapannati; and Umasvati (c. 150 BCE), who, although better known for his influential writings on Jaina philosophy and metaphysics, composed a mathematical work calledTattwarthadhigama-Sutra Bhashya.
Oral tradition[edit]
Mathematicians of ancient and early medieval India were almost all Sanskrit pandits (paṇḍita "learned man"),[38] who were trained in Sanskrit language and literature, and possessed "a common stock of knowledge in grammar (vyākaraṇa), exegesis (mīmāṃsā) and logic (nyāya)."[38] Memorization of "what is heard" (śruti in Sanskrit) through recitation played a major role in the transmission of sacred texts in ancient India. Memorization and recitation was also used to transmit philosophical and literary works, as well as treatises on ritual and grammar. Modern scholars of ancient India have noted the "truly remarkable achievements of the Indian pandits who have preserved enormously bulky texts orally for millennia."[39]
Styles of memorisation[edit]
Prodigous energy was expended by ancient Indian culture in ensuring that these texts were transmitted from generation to generation with inordinate fidelity.[40] For example, memorisation of the sacred Vedas included up to eleven forms of recitation of the same text. The texts were subsequently "proof-read" by comparing the different recited versions. Forms of recitation included the jaṭā-pāṭha (literally "mesh recitation") in which every two adjacent words in the text were first recited in their original order, then repeated in the reverse order, and finally repeated again in the original order.[41] The recitation thus proceeded as:
In another form of recitation, dhvaja-pāṭha[41] (literally "flag recitation") a sequence of N words were recited (and memorised) by pairing the first two and last two words and then proceeding as:
The most complex form of recitation, ghana-pāṭha (literally "dense recitation"), according to (Filliozat 2004, p. 139), took the form:
That these methods have been effective, is testified to by the preservation of the most ancient Indian religious text, the Ṛgveda (ca. 1500 BCE), as a single text, without any variant readings.[41] Similar methods were used for memorising mathematical texts, whose transmission remained exclusively oral until the end of the Vedic period (ca. 500 BCE).
The Sūtra genre[edit]
Mathematical activity in ancient India began as a part of a "methodological reflexion" on the sacred Vedas, which took the form of works called Vedāṇgas, or, "Ancillaries of the Veda" (7th–4th century BCE).[42] The need to conserve the sound of sacred text by use of śikṣā (phonetics) and chhandas (metrics); to conserve its meaning by use of vyākaraṇa(grammar) and nirukta (etymology); and to correctly perform the rites at the correct time by the use of kalpa (ritual) and jyotiṣa (astronomy), gave rise to the six disciplines of theVedāṇgas.[42] Mathematics arose as a part of the last two disciplines, ritual and astronomy (which also included astrology). Since the Vedāṇgas immediately preceded the use of writing in ancient India, they formed the last of the exclusively oral literature. They were expressed in a highly compressed mnemonic form, the sūtra (literally, "thread"):
The knowers of the sūtra know it as having few phonemes, being devoid of ambiguity, containing the essence, facing everything, being without pause and unobjectionable.[42]
Extreme brevity was achieved through multiple means, which included using ellipsis "beyond the tolerance of natural language,"[42] using technical names instead of longer descriptive names, abridging lists by only mentioning the first and last entries, and using markers and variables.[42] The sūtras create the impression that communication through the text was "only a part of the whole instruction. The rest of the instruction must have been transmitted by the so-called Guru-shishya parampara, 'uninterrupted succession from teacher (guru) to the student (śisya),' and it was not open to the general public" and perhaps even kept secret.[43] The brevity achieved in a sūtra is demonstrated in the following example from the Baudhāyana Śulba Sūtra (700 BCE).
The domestic fire-altar in the Vedic period was required by ritual to have a square base and be constituted of five layers of bricks with 21 bricks in each layer. One method of constructing the altar was to divide one side of the square into three equal parts using a cord or rope, to next divide the transverse (or perpendicular) side into seven equal parts, and thereby sub-divide the square into 21 congruent rectangles. The bricks were then designed to be of the shape of the constituent rectangle and the layer was created. To form the next layer, the same formula was used, but the bricks were arranged transversely.[44] The process was then repeated three more times (with alternating directions) in order to complete the construction. In the Baudhāyana Śulba Sūtra, this procedure is described in the following words:
"II.64. After dividing the quadri-lateral in seven, one divides the transverse [cord] in three.
II.65. In another layer one places the [bricks] North-pointing."[44]
According to (Filliozat 2004, p. 144), the officiant constructing the altar has only a few tools and materials at his disposal: a cord (Sanskrit, rajju, f.), two pegs (Sanskrit, śanku, m.), and clay to make the bricks (Sanskrit, iṣṭakā, f.). Concision is achieved in the sūtra, by not explicitly mentioning what the adjective "transverse" qualifies; however, from the feminine form of the (Sanskrit) adjective used, it is easily inferred to qualify "cord." Similarly, in the second stanza, "bricks" are not explicitly mentioned, but inferred again by the feminine plural form of "North-pointing." Finally, the first stanza, never explicitly says that the first layer of bricks are oriented in the East-West direction, but that too is implied by the explicit mention of "North-pointing" in the second stanza; for, if the orientation was meant to be the same in the two layers, it would either not be mentioned at all or be only mentioned in the first stanza. All these inferences are made by the officiant as he recalls the formula from his memory.[44]
The written tradition: prose commentary[edit]
With the increasing complexity of mathematics and other exact sciences, both writing and computation were required. Consequently, many mathematical works began to be written down in manuscripts that were then copied and re-copied from generation to generation.
"India today is estimated to have about thirty million manuscripts, the largest body of handwritten reading material anywhere in the world. The literate culture of Indian science goes back to at least the fifth century B.C. ... as is shown by the elements of Mesopotamian omen literature and astronomy that entered India at that time and (were) definitely not ... preserved orally."[45]
The earliest mathematical prose commentary was that on the work, Āryabhaṭīya (written 499 CE), a work on astronomy and mathematics. The mathematical portion of theĀryabhaṭīya was composed of 33 sūtras (in verse form) consisting of mathematical statements or rules, but without any proofs.[46] However, according to (Hayashi 2003, p. 123), "this does not necessarily mean that their authors did not prove them. It was probably a matter of style of exposition." From the time of Bhaskara I (600 CE onwards), prose commentaries increasingly began to include some derivations (upapatti). Bhaskara I's commentary on the Āryabhaṭīya, had the following structure:[46]
- Rule ('sūtra') in verse by Āryabhaṭa
- Commentary by Bhāskara I, consisting of:
- Elucidation of rule (derivations were still rare then, but became more common later)
- Example (uddeśaka) usually in verse.
- Setting (nyāsa/sthāpanā) of the numerical data.
- Working (karana) of the solution.
- Verification (pratyayakaraṇa, literally "to make conviction") of the answer. These became rare by the 13th century, derivations or proofs being favoured by then.[46]
Typically, for any mathematical topic, students in ancient India first memorised the sūtras, which, as explained earlier, were "deliberately inadequate"[45] in explanatory details (in order to pithily convey the bare-bone mathematical rules). The students then worked through the topics of the prose commentary by writing (and drawing diagrams) on chalk- and dust-boards (i.e. boards covered with dust). The latter activity, a staple of mathematical work, was to later prompt mathematician-astronomer, Brahmagupta (fl. 7th century CE), to characterize astronomical computations as "dust work" (Sanskrit: dhulikarman).[47]
Numerals and the decimal numeral system[edit]
The earliest decimal system, using Egyptian hieroglyphs, dates back to 3000 BC,[48] but the modern numeration system was first recorded in India, where it was transmitted to the Islamic world, and eventually to Europe.[49] The Syrian bishop Severus Sebokht wrote in the mid-7th century CE about the "nine signs" of the Indians for expressing numbers.[49]However, how, when, and where the first decimal place value system was invented is not so clear.[50]
The earliest extant script used in India was the Kharoṣṭhī script used in the Gandhara culture of the north-west. It is thought to be of Aramaic origin and it was in use from the 4th century BCE to the 4th century CE. Almost contemporaneously, another script, the Brāhmī script, appeared on much of the sub-continent, and would later become the foundation of many scripts of South Asia and South-east Asia. Both scripts had numeral symbols and numeral systems, which were initially not based on a place-value system.[51]
The earliest surviving evidence of decimal place value numerals in India and southeast Asia is from the middle of the first millennium CE.[52] A copper plate from Gujarat, India mentions the date 595 CE, written in a decimal place value notation, although there is some doubt as to the authenticity of the plate.[52] Decimal numerals recording the years 683 CE have also been found in stone inscriptions in Indonesia and Cambodia, where Indian cultural influence was substantial.[52]
There are older textual sources, although the extant manuscript copies of these texts are from much later dates.[53] Probably the earliest such source is the work of the Buddhist philosopher Vasumitra dated likely to the 1st century CE.[53] Discussing the counting pits of merchants, Vasumitra remarks, "When [the same] clay counting-piece is in the place of units, it is denoted as one, when in hundreds, one hundred."[53] Although such references seem to imply that his readers had knowledge of a decimal place value representation, the "brevity of their allusions and the ambiguity of their dates, however, do not solidly establish the chronology of the development of this concept."[53]
A third decimal representation was employed in a verse composition technique, later labelled Bhuta-sankhya (literally, "object numbers") used by early Sanskrit authors of technical books.[54] Since many early technical works were composed in verse, numbers were often represented by objects in the natural or religious world that correspondence to them; this allowed a many-to-one correspondence for each number and made verse composition easier.[54] According to Plofker 2009, the number 4, for example, could be represented by the word "Veda" (since there were four of these religious texts), the number 32 by the word "teeth" (since a full set consists of 32), and the number 1 by "moon" (since there is only one moon).[54] So, Veda/teeth/moon would correspond to the decimal numeral 1324, as the convention for numbers was to enumerate their digits from right to left.[54] The earliest reference employing object numbers is a ca. 269 CE Sanskrit text, Yavanajātaka (literally "Greek horoscopy") of Sphujidhvaja, a versification of an earlier (ca. 150 CE) Indian prose adaptation of a lost work of Hellenistic astrology.[55] Such use seems to make the case that by the mid-3rd century CE, the decimal place value system was familiar, at least to readers of astronomical and astrological texts in India.[54]
It has been hypothesized that the Indian decimal place value system was based on the symbols used on Chinese counting boards from as early as the middle of the first millennium BCE.[56] According to Plofker 2009,
These counting boards, like the Indian counting pits, ..., had a decimal place value structure ... Indians may well have learned of these decimal place value "rod numerals" from Chinese Buddhist pilgrims or other travelers, or they may have developed the concept independently from their earlier non-place-value system; no documentary evidence survives to confirm either conclusion."[56]
Bakhshali Manuscript[edit]
The oldest extant mathematical manuscript in South Asia is the Bakhshali Manuscript, a birch bark manuscript written in "Buddhist hybrid Sanskrit"[13] in the Śāradā script, which was used in the northwestern region of the Indian subcontinent between the 8th and 12th centuries CE.[57] The manuscript was discovered in 1881 by a farmer while digging in a stone enclosure in the village of Bakhshali, near Peshawar (then in British India and now in Pakistan). Of unknown authorship and now preserved in the Bodleian Library in Oxford University, the manuscript has been variously dated—as early as the "early centuries of the Christian era"[58] and as late as between the 9th and 12th century CE.[59] The 7th century CE is now considered a plausible date,[60] albeit with the likelihood that the "manuscript in its present-day form constitutes a commentary or a copy of an anterior mathematical work."[61]
The surviving manuscript has seventy leaves, some of which are in fragments. Its mathematical content consists of rules and examples, written in verse, together with prose commentaries, which include solutions to the examples.[57] The topics treated include arithmetic (fractions, square roots, profit and loss, simple interest, the rule of three, andregula falsi) and algebra (simultaneous linear equations and quadratic equations), and arithmetic progressions. In addition, there is a handful of geometric problems (including problems about volumes of irregular solids). The Bakhshali manuscript also "employs a decimal place value system with a dot for zero."[57] Many of its problems are the so-called equalization problems that lead to systems of linear equations. One example from Fragment III-5-3v is the following:
"One merchant has seven asava horses, a second has nine haya horses, and a third has ten camels. They are equally well off in the value of their animals if each gives two animals, one to each of the others. Find the price of each animal and the total value for the animals possessed by each merchant."[62]
The prose commentary accompanying the example solves the problem by converting it to three (under-determined) equations in four unknowns and assuming that the prices are all integers.[62]
Classical Period (400–1200)[edit]
This period is often known as the golden age of Indian Mathematics. This period saw mathematicians such as Aryabhata, Varahamihira, Brahmagupta, Bhaskara I, Mahavira, andBhaskara II give broader and clearer shape to many branches of mathematics. Their contributions would spread to Asia, the Middle East, and eventually to Europe. Unlike Vedic mathematics, their works included both astronomical and mathematical contributions. In fact, mathematics of that period was included in the 'astral science' (jyotiḥśāstra) and consisted of three sub-disciplines: mathematical sciences (gaṇita or tantra), horoscope astrology (horā or jātaka) and divination (saṃhitā).[47] This tripartite division is seen in Varāhamihira's 6th century compilation—Pancasiddhantika[63] (literally panca, "five," siddhānta, "conclusion of deliberation", dated 575 CE)—of five earlier works, Surya Siddhanta,Romaka Siddhanta, Paulisa Siddhanta, Vasishtha Siddhanta and Paitamaha Siddhanta, which were adaptations of still earlier works of Mesopotamian, Greek, Egyptian, Roman and Indian astronomy. As explained earlier, the main texts were composed in Sanskrit verse, and were followed by prose commentaries.[47]
Fifth and sixth centuries[edit]
- Surya Siddhanta
Though its authorship is unknown, the Surya Siddhanta (c. 400) contains the roots of modern trigonometry.[citation needed] Because it contains many words of foreign origin, some authors consider that it was written under the influence of Mesopotamia and Greece.[64]
This ancient text uses the following as trigonometric functions for the first time:[citation needed]
- Sine (Jya).
- Cosine (Kojya).
- Inverse sine (Otkram jya).
It also contains the earliest uses of:[citation needed]
Later Indian mathematicians such as Aryabhata made references to this text, while later Arabic and Latin translations were very influential in Europe and the Middle East.
- Chhedi calendar
This Chhedi calendar (594) contains an early use of the modern place-value Hindu-Arabic numeral system now used universally (see also Hindu-Arabic numerals).
- Aryabhata I
Aryabhata (476–550) wrote the Aryabhatiya. He described the important fundamental principles of mathematics in 332 shlokas. The treatise contained:
- Quadratic equations
- Trigonometry
- The value of π, correct to 4 decimal places.
Aryabhata also wrote the Arya Siddhanta, which is now lost. Aryabhata's contributions include:
Trigonometry:
(See also : Aryabhata's sine table)
- Introduced the trigonometric functions.
- Defined the sine (jya) as the modern relationship between half an angle and half a chord.
- Defined the cosine (kojya).
- Defined the versine (utkrama-jya).
- Defined the inverse sine (otkram jya).
- Gave methods of calculating their approximate numerical values.
- Contains the earliest tables of sine, cosine and versine values, in 3.75° intervals from 0° to 90°, to 4 decimal places of accuracy.
- Contains the trigonometric formula sin(n + 1)x − sin nx = sin nx − sin(n − 1)x − (1/225)sin nx.
- Spherical trigonometry.
Arithmetic:
Algebra:
- Solutions of simultaneous quadratic equations.
- Whole number solutions of linear equations by a method equivalent to the modern method.
- General solution of the indeterminate linear equation .
Mathematical astronomy:
- Accurate calculations for astronomical constants, such as the:
- Solar eclipse.
- Lunar eclipse.
- The formula for the sum of the cubes, which was an important step in the development of integral calculus.[65]
- Varahamihira
Varahamihira (505–587) produced the Pancha Siddhanta (The Five Astronomical Canons). He made important contributions to trigonometry, including sine and cosine tables to 4 decimal places of accuracy and the following formulas relating sine and cosine functions:
Seventh and eighth centuries[edit]
In the 7th century, two separate fields, arithmetic (which included mensuration) and algebra, began to emerge in Indian mathematics. The two fields would later be called pāṭī-gaṇita (literally "mathematics of algorithms") and bīja-gaṇita (lit. "mathematics of seeds," with "seeds"—like the seeds of plants—representing unknowns with the potential to generate, in this case, the solutions of equations).[66] Brahmagupta, in his astronomical work Brāhma Sphuṭa Siddhānta (628 CE), included two chapters (12 and 18) devoted to these fields. Chapter 12, containing 66 Sanskrit verses, was divided into two sections: "basic operations" (including cube roots, fractions, ratio and proportion, and barter) and "practical mathematics" (including mixture, mathematical series, plane figures, stacking bricks, sawing of timber, and piling of grain).[67] In the latter section, he stated his famous theorem on the diagonals of a cyclic quadrilateral:[67]
Brahmagupta's theorem: If a cyclic quadrilateral has diagonals that are perpendicular to each other, then the perpendicular line drawn from the point of intersection of the diagonals to any side of the quadrilateral always bisects the opposite side.
Chapter 12 also included a formula for the area of a cyclic quadrilateral (a generalisation of Heron's formula), as well as a complete description of rational triangles (i.e. triangles with rational sides and rational areas).
Brahmagupta's formula: The area, A, of a cyclic quadrilateral with sides of lengths a, b, c, d, respectively, is given by
where s, the semiperimeter, given by 

Brahmagupta's Theorem on rational triangles: A triangle with rational sides 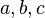 and rational area is of the form:
and rational area is of the form:
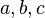 and rational area is of the form:
and rational area is of the form:
Chapter 18 contained 103 Sanskrit verses which began with rules for arithmetical operations involving zero and negative numbers[67] and is considered the first systematic treatment of the subject. The rules (which included 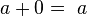 and
and 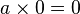 ) were all correct, with one exception:
) were all correct, with one exception:  .[67] Later in the chapter, he gave the first explicit (although still not completely general) solution of the quadratic equation:
.[67] Later in the chapter, he gave the first explicit (although still not completely general) solution of the quadratic equation:
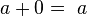 and
and 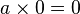 ) were all correct, with one exception:
) were all correct, with one exception:  .[67] Later in the chapter, he gave the first explicit (although still not completely general) solution of the quadratic equation:
.[67] Later in the chapter, he gave the first explicit (although still not completely general) solution of the quadratic equation:| “ | To the absolute number multiplied by four times the [coefficient of the] square, add the square of the [coefficient of the] middle term; the square root of the same, less the [coefficient of the] middle term, being divided by twice the [coefficient of the] square is the value. | ” |
This is equivalent to:
Also in chapter 18, Brahmagupta was able to make progress in finding (integral) solutions of Pell's equation,[70]
where 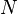 is a nonsquare integer. He did this by discovering the following identity:[70]
is a nonsquare integer. He did this by discovering the following identity:[70]
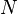 is a nonsquare integer. He did this by discovering the following identity:[70]
is a nonsquare integer. He did this by discovering the following identity:[70]
Brahmagupta's Identity:  which was a generalization of an earlier identity of Diophantus:[70]Brahmagupta used his identity to prove the following lemma:[70]
which was a generalization of an earlier identity of Diophantus:[70]Brahmagupta used his identity to prove the following lemma:[70]
 which was a generalization of an earlier identity of Diophantus:[70]Brahmagupta used his identity to prove the following lemma:[70]
which was a generalization of an earlier identity of Diophantus:[70]Brahmagupta used his identity to prove the following lemma:[70]
Lemma (Brahmagupta): If  is a solution of
is a solution of  and,
and, 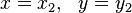 is a solution of
is a solution of  , then:
, then:
 is a solution of
is a solution of  and,
and, 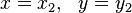 is a solution of
is a solution of  , then:
, then: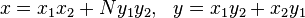 is a solution of
is a solution of 
He then used this lemma to both generate infinitely many (integral) solutions of Pell's equation, given one solution, and state the following theorem:
Theorem (Brahmagupta): If the equation 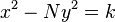 has an integer solution for any one of
has an integer solution for any one of  then Pell's equation:
then Pell's equation:
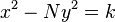 has an integer solution for any one of
has an integer solution for any one of  then Pell's equation:
then Pell's equation:
also has an integer solution.[71]
Brahmagupta did not actually prove the theorem, but rather worked out examples using his method. The first example he presented was:[70]
Example (Brahmagupta): Find integers  such that:
such that:
 such that:
such that:
In his commentary, Brahmagupta added, "a person solving this problem within a year is a mathematician."[70] The solution he provided was:
- Bhaskara I
Bhaskara I (c. 600–680) expanded the work of Aryabhata in his books titled Mahabhaskariya, Aryabhatiya-bhashya and Laghu-bhaskariya. He produced:
- Solutions of indeterminate equations.
- A rational approximation of the sine function.
- A formula for calculating the sine of an acute angle without the use of a table, correct to two decimal places.
Ninth to twelfth centuries[edit]
- Virasena
Virasena (9th century) was a Jain mathematician in the court of Rashtrakuta King Amoghavarsha of Manyakheta, Karnataka. He wrote the Dhavala, a commentary on Jain mathematics, which:
- Deals with the concept of ardhaccheda, the number of times a number could be halved; effectively logarithms to base 2, and lists various rules involving this operation.[72][73]
- First uses logarithms to base 3 (trakacheda) and base 4 (caturthacheda).
Virasena also gave:
It is thought that much of the mathematical material in the Dhavala can attributed to previous writers, especially Kundakunda, Shamakunda, Tumbulura, Samantabhadra and Bappadeva and date who wrote between 200 and 600 AD.[73]
- Mahavira
Mahavira Acharya (c. 800–870) from Karnataka, the last of the notable Jain mathematicians, lived in the 9th century and was patronised by the Rashtrakuta king Amoghavarsha. He wrote a book titled Ganit Saar Sangraha on numerical mathematics, and also wrote treatises about a wide range of mathematical topics. These include the mathematics of:
- Zero
- Squares
- Cubes
- square roots, cube roots, and the series extending beyond these
- Plane geometry
- Solid geometry
- Problems relating to the casting of shadows
- Formulae derived to calculate the area of an ellipse and quadrilateral inside a circle.
Mahavira also:
- Asserted that the square root of a negative number did not exist
- Gave the sum of a series whose terms are squares of an arithmetical progression, and gave empirical rules for area and perimeter of an ellipse.
- Solved cubic equations.
- Solved quartic equations.
- Solved some quintic equations and higher-order polynomials.
- Gave the general solutions of the higher order polynomial equations:
- Solved indeterminate quadratic equations.
- Solved indeterminate cubic equations.
- Solved indeterminate higher order equations.
- Shridhara
Shridhara (c. 870–930), who lived in Bengal, wrote the books titled Nav Shatika, Tri Shatika and Pati Ganita. He gave:
- A good rule for finding the volume of a sphere.
- The formula for solving quadratic equations.
The Pati Ganita is a work on arithmetic and mensuration. It deals with various operations, including:
- Elementary operations
- Extracting square and cube roots.
- Fractions.
- Eight rules given for operations involving zero.
- Methods of summation of different arithmetic and geometric series, which were to become standard references in later works.
- Manjula
Aryabhata's differential equations were elaborated in the 10th century by Manjula (also Munjala), who realised that the expression[74]
could be approximately expressed as
He understood the concept of differentiation after solving the differential equation that resulted from substituting this expression into Aryabhata's differential equation.[74]
- Aryabhata II
Aryabhata II (c. 920–1000) wrote a commentary on Shridhara, and an astronomical treatise Maha-Siddhanta. The Maha-Siddhanta has 18 chapters, and discusses:
- Numerical mathematics (Ank Ganit).
- Algebra.
- Solutions of indeterminate equations (kuttaka).
- Shripati
Shripati Mishra (1019–1066) wrote the books Siddhanta Shekhara, a major work on astronomy in 19 chapters, and Ganit Tilaka, an incomplete arithmetical treatise in 125 verses based on a work by Shridhara. He worked mainly on:
- Permutations and combinations.
- General solution of the simultaneous indeterminate linear equation.
He was also the author of Dhikotidakarana, a work of twenty verses on:
The Dhruvamanasa is a work of 105 verses on:
- Calculating planetary longitudes
- eclipses.
- planetary transits.
- Nemichandra Siddhanta Chakravati
Nemichandra Siddhanta Chakravati (c. 1100) authored a mathematical treatise titled Gome-mat Saar.
- Bhaskara II
Bhāskara II (1114–1185) was a mathematician-astronomer who wrote a number of important treatises, namely the Siddhanta Shiromani, Lilavati, Bijaganita, Gola Addhaya, Griha Ganitam and Karan Kautoohal. A number of his contributions were later transmitted to the Middle East and Europe. His contributions include:
Arithmetic:
- Interest computation
- Arithmetical and geometrical progressions
- Plane geometry
- Solid geometry
- The shadow of the gnomon
- Solutions of combinations
- Gave a proof for division by zero being infinity.
Algebra:
- The recognition of a positive number having two square roots.
- Surds.
- Operations with products of several unknowns.
- The solutions of:
- Quadratic equations.
- Cubic equations.
- Quartic equations.
- Equations with more than one unknown.
- Quadratic equations with more than one unknown.
- The general form of Pell's equation using the chakravala method.
- The general indeterminate quadratic equation using the chakravala method.
- Indeterminate cubic equations.
- Indeterminate quartic equations.
- Indeterminate higher-order polynomial equations.
Geometry:
- Gave a proof of the Pythagorean theorem.
Calculus:
- Conceived of differential calculus.
- Discovered the derivative.
- Discovered the differential coefficient.
- Developed differentiation.
- Stated Rolle's theorem, a special case of the mean value theorem (one of the most important theorems of calculus and analysis).
- Derived the differential of the sine function.
- Computed π, correct to five decimal places.
- Calculated the length of the Earth's revolution around the Sun to 9 decimal places.
Trigonometry:
- Developments of spherical trigonometry
- The trigonometric formulas:
Kerala mathematics (1300–1600)[edit]
Main article: Kerala school of astronomy and mathematics
The Kerala school of astronomy and mathematics was founded by Madhava of Sangamagrama in Kerala, South India and included among its members: Parameshvara, Neelakanta Somayaji, Jyeshtadeva, Achyuta Pisharati, Melpathur Narayana Bhattathiri and Achyuta Panikkar. It flourished between the 14th and 16th centuries and the original discoveries of the school seems to have ended with Narayana Bhattathiri (1559–1632). In attempting to solve astronomical problems, the Kerala school astronomers independently created a number of important mathematics concepts. The most important results, series expansion for trigonometric functions, were given in Sanskrit verse in a book by Neelakanta calledTantrasangraha and a commentary on this work called Tantrasangraha-vakhya of unknown authorship. The theorems were stated without proof, but proofs for the series for sine,cosine, and inverse tangent were provided a century later in the work Yuktibhāṣā (c.1500–c.1610), written in Malayalam, by Jyesthadeva, and also in a commentary onTantrasangraha.[75]
Their discovery of these three important series expansions of calculus—several centuries before calculus was developed in Europe by Isaac Newton and Gottfried Leibniz—was an achievement. However, the Kerala School did not invent calculus,[76] because, while they were able to develop Taylor series expansions for the important trigonometric functions,differentiation, term by term integration, convergence tests, iterative methods for solutions of non-linear equations, and the theory that the area under a curve is its integral, they developed neither a theory of differentiation or integration, nor the fundamental theorem of calculus.[77] The results obtained by the Kerala school include:
- The (infinite) geometric series:
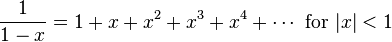 [78] This formula was already known, for example, in the work of the 10th-century Arab mathematician Alhazen (the Latinized form of the name Ibn Al-Haytham (965–1039)).[79]
[78] This formula was already known, for example, in the work of the 10th-century Arab mathematician Alhazen (the Latinized form of the name Ibn Al-Haytham (965–1039)).[79] - A semi-rigorous proof (see "induction" remark below) of the result:
 for large n. This result was also known to Alhazen.[75]
for large n. This result was also known to Alhazen.[75] - Intuitive use of mathematical induction, however, the inductive hypothesis was not formulated or employed in proofs.[75]
- Applications of ideas from (what was to become) differential and integral calculus to obtain (Taylor–Maclaurin) infinite series for
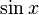 ,
,  , and
, and 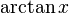 [76] TheTantrasangraha-vakhya gives the series in verse, which when translated to mathematical notation, can be written as:[75]
[76] TheTantrasangraha-vakhya gives the series in verse, which when translated to mathematical notation, can be written as:[75]
-
- where, for r = 1, the series reduces to the standard power series for these trigonometric functions, for example:
- and
- Use of rectification (computation of length) of the arc of a circle to give a proof of these results. (The later method of Leibniz, using quadrature (i.e. computation of area under the arc of the circle, was not used.)[75]
- Use of series expansion of
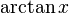 to obtain an infinite series expression (later known as Gregory series) for
to obtain an infinite series expression (later known as Gregory series) for 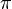 :[75]
:[75]
- A rational approximation of error for the finite sum of their series of interest. For example, the error,
 , (for n odd, and i = 1, 2, 3) for the series:
, (for n odd, and i = 1, 2, 3) for the series:
- Manipulation of error term to derive a faster converging series for
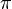 :[75]
:[75]
- Using the improved series to derive a rational expression,[75] 104348/33215 for π correct up to nine decimal places, i.e. 3.141592653.
- Use of an intuitive notion of limit to compute these results.[75]
- A semi-rigorous (see remark on limits above) method of differentiation of some trigonometric functions.[77] However, they did not formulate the notion of a function, or have knowledge of the exponential or logarithmic functions.
The works of the Kerala school were first written up for the Western world by Englishman C.M. Whish in 1835. According to Whish, the Kerala mathematicians had "laid the foundation for a complete system of fluxions" and these works abounded "with fluxional forms and series to be found in no work of foreign countries."[80]
However, Whish's results were almost completely neglected, until over a century later, when the discoveries of the Kerala school were investigated again by C. Rajagopal and his associates. Their work includes commentaries on the proofs of the arctan series in Yuktibhāṣā given in two papers,[81][82] a commentary on the Yuktibhāṣā's proof of the sine and cosine series[83] and two papers that provide the Sanskrit verses of the Tantrasangrahavakhya for the series for arctan, sin, and cosine (with English translation and commentary).[84][85]
The Kerala mathematicians included Narayana Pandit[dubious ] (c. 1340–1400), who composed two works, an arithmetical treatise, Ganita Kaumudi, and an algebraic treatise, Bijganita Vatamsa. Narayana is also thought to be the author of an elaborate commentary of Bhaskara II's Lilavati, titled Karmapradipika (or Karma-Paddhati). Madhava of Sangamagrama (c. 1340–1425) was the founder of the Kerala School. Although it is possible that he wrote Karana Paddhati a work written sometime between 1375 and 1475, all we really know of his work comes from works of later scholars.
Parameshvara (c. 1370–1460) wrote commentaries on the works of Bhaskara I, Aryabhata and Bhaskara II. His Lilavati Bhasya, a commentary on Bhaskara II's Lilavati, contains one of his important discoveries: a version of the mean value theorem. Nilakantha Somayaji (1444–1544) composed the Tantra Samgraha (which 'spawned' a later anonymous commentary Tantrasangraha-vyakhya and a further commentary by the name Yuktidipaika, written in 1501). He elaborated and extended the contributions of Madhava.
Citrabhanu (c. 1530) was a 16th-century mathematician from Kerala who gave integer solutions to 21 types of systems of two simultaneous algebraic equations in two unknowns. These types are all the possible pairs of equations of the following seven forms:
For each case, Citrabhanu gave an explanation and justification of his rule as well as an example. Some of his explanations are algebraic, while others are geometric. Jyesthadeva(c. 1500–1575) was another member of the Kerala School. His key work was the Yukti-bhāṣā (written in Malayalam, a regional language of Kerala). Jyesthadeva presented proofs of most mathematical theorems and infinite series earlier discovered by Madhava and other Kerala School mathematicians.
Charges of Eurocentrism[edit]
It has been suggested that Indian contributions to mathematics have not been given due acknowledgement in modern history and that many discoveries and inventions by Indian mathematicians were known to their Western counterparts, copied by them, and presented as their own original work; and further, that this mass plagiarism has gone unrecognised due to Eurocentrism. According to G. G. Joseph:
[Their work] takes on board some of the objections raised about the classical Eurocentric trajectory. The awareness [of Indian and Arabic mathematics] is all too likely to be tempered with dismissive rejections of their importance compared to Greek mathematics. The contributions from other civilisations – most notably China and India, are perceived either as borrowers from Greek sources or having made only minor contributions to mainstream mathematical development. An openness to more recent research findings, especially in the case of Indian and Chinese mathematics, is sadly missing"[86]
The historian of mathematics, Florian Cajori, suggested that he and others "suspect that Diophantus got his first glimpse of algebraic knowledge from India."[87] However, he also wrote that "it is certain that portions of Hindu mathematics are of Greek origin".[88]
More recently, as discussed in the above section, the infinite series of calculus for trigonometric functions (rediscovered by Gregory, Taylor, and Maclaurin in the late 17th century) were described (with proofs) in India, by mathematicians of the Kerala school, remarkably some two centuries earlier. Some scholars have recently suggested that knowledge of these results might have been transmitted to Europe through the trade route from Kerala by traders and Jesuit missionaries.[89] Kerala was in continuous contact with China andArabia, and, from around 1500, with Europe. The existence of communication routes and a suitable chronology certainly make such a transmission a possibility. However, there is no direct evidence by way of relevant manuscripts that such a transmission actually took place.[89] According to David Bressoud, "there is no evidence that the Indian work of series was known beyond India, or even outside of Kerala, until the nineteenth century."[76][90]
Both Arab and Indian scholars made discoveries before the 17th century that are now considered a part of calculus.[77] However, they were not able to, as Newton and Leibniz were, to "combine many differing ideas under the two unifying themes of the derivative and the integral, show the connection between the two, and turn calculus into the great problem-solving tool we have today."[77] The intellectual careers of both Newton and Leibniz are well-documented and there is no indication of their work not being their own;[77] however, it is not known with certainty whether the immediate predecessors of Newton and Leibniz, "including, in particular, Fermat and Roberval, learned of some of the ideas of the Islamic and Indian mathematicians through sources we are not now aware."[77] This is an active area of current research, especially in the manuscripts collections of Spain and Maghreb, research that is now being pursued, among other places, at the Centre National de Recherche Scientifique in Paris.[77]



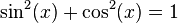

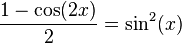


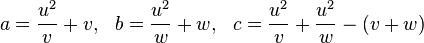
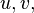 and
and 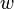 .
.
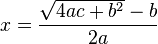



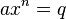



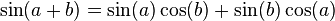



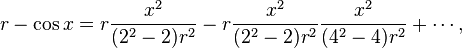





![\begin{align}
& x + y = a,\ x - y = b,\ xy = c, x^2 + y^2 = d, \\[8pt]
& x^2 - y^2 = e,\ x^3 + y^3 = f,\ x^3 - y^3 = g
\end{align}](http://upload.wikimedia.org/math/8/0/f/80fc0f52028031170c8d4b41617959b1.png)
No comments:
Post a Comment